
Datenaufbereitung
Die Frequenz-Zeit-Unschärfe der Fourier-Transformation
Ein spürbares Problem der Auswertung des Radar-Signals ist etwas, das man als "Frequenz-Zeit-Unschärfe" bezeichnen kann. Im folgenden sei N die Zahl der für eine Fourier-Transformation aufgenommenen Datenpunkte.
Die Fourier-Transformation bestimmt den Anteil der n-Einheitswurzeln am Signal:
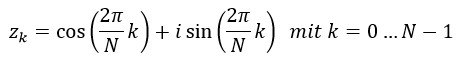
Daraus sieht man, dass der Frequenz-Abstand zwischen den einzelnen Fourier-Frequenzen, unter Beachtung, dass die Zeit zwischen zwei Datenpunkten nicht 1 ist, sondern der Sampling-Zeit entspricht:
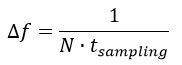
Man sieht also, dass man, will man ein genaues Fourier-Spektrum aufnehmen, viele Datenpunkte braucht. Jeder Datenpunkt dauert jedoch einmal die Sampling-Zeit, um aufgenommen zu werden. Einen Datensatz für die Fourier-Transformation zu gewinnen dauert also:
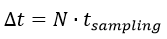
In diesem Zeitintervall jedoch bestimmt die Fourier-Transformation nur die Stärke, mit der die einzelnen Frequenzen vorgekommen sind, nicht jedoch den Zeitpunkt ihres Auftretens innerhalb des Zeitfensters. Daher kann nicht festgestellt werden, wann eine Frequenz (und damit letztendlich eine Bewegung in dieser Anwendung) aufgetreten ist, nur dass sie innerhalb des Zeitfensters geschehen ist. Im Idealfall will man also das Zeitfenster möglichst klein halten, um den Zeitpunkt einer Bewegung klar ausmachen zu können. Gleichzeitig besteht jedoch weiterhin der Wunsch, die Frequenz möglichst exakt zu bestimmen. Aus oben gefundenen Formeln entsteht folgendes Gesetz:
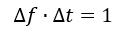
Dies ist eine Formulierung des Gabor-Limits.
An diesem sieht man nun, dass weder über die Sampling-Rate, noch über die Zahl der aufgenommenen Datenpunkte ein Optimum aus Frequenzgenauigkeit und Zeitgenauigkeit gefunden werden kann, man kann nur eines auf Kosten des anderen exakter machen. Das hat für unsere Anwendung harte Konsequenzen. Ändert ein Objekt seine Geschwindigkeit, so wandert der Frequenz-Peak durch das Fourier-Spektrum. Da jedoch ein ganzes Zeitintervall aufgenommen werden muss, sieht man nicht einen wandernden Peak, sondern ein Plateau, aus dem weder die genaue Geschwindigkeit, noch das genaue Auftreten der Bewegung bestimmt werden kann.
Lösungsansätze
Ein Lösungsansatz wäre natürlich, die Radar-Frequenz höher zu setzen, so dass der Frequenzunterschied bei einer Geschwindigkeitsänderung von 1 km/h so groß ist, dass die Frequenzungenauigkeit nicht ins Gewicht fällt. Da das jedoch (bei Beibehaltung dieses Radar-Moduls) kaum möglich ist, muss an der Natur der Transformation gearbeitet werden.
Das Problem der Lokalisierung eines Signals innerhalb des Transformations-Zeitfensters ist nicht neu. Die Idee, die hier immer wieder Anwendung findet, kann das Problem der Frequenz-Zeit-Unschärfe nicht beheben, jedoch geschickt umgehen. Als Grundansatz dient, das Fourier-Zeitfenster frequenzabhängig größer/kleiner zu machen. Das bedeutet, dass man niedrige Frequenzen, deren zeitliche Lokalisierung nicht sonderlich exakt sein muss, sehr genau in der Frequenz bestimmt, während hohe Frequenzen, wo ein paar Hz Unterschied nicht mehr sonderlich relevant sind, sehr genau temporal lokalisiert werden.
Die Wavelet-Transformation
Ein Ansatz ist die Wavelet-Transformation, die aus der Bildkompression bekannt ist. Die Wavelet-Transformation erstellt kleine Frequenz-Pakete (sog. Wavelets), die in Frequenz und Position geändert werden.
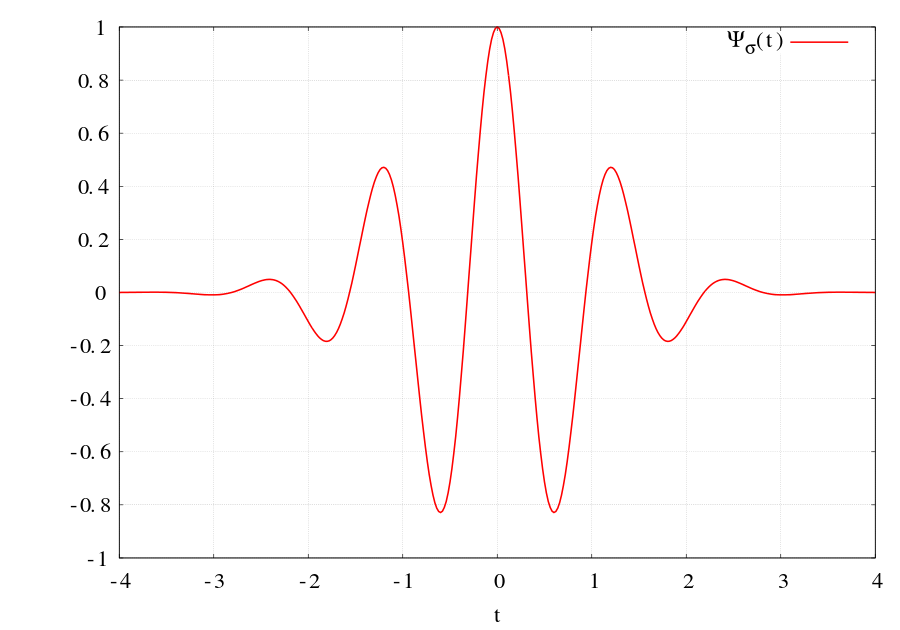
Dann wird ihr Auftreten innerhalb des Signals untersucht. Die Diskretisierung der Schritte, mit denen das Wavelet seine Position ändert, ist dabei frequenzabhängig. Hiermit wird die zuvor angesprochene Idee umgesetzt, bei niedrigen Frequenzen exakt im Frequenzbereich und ungenau im zeitlichen Bereich zu sein, und entsprechend umgekehrt für hohe Frequenzen.
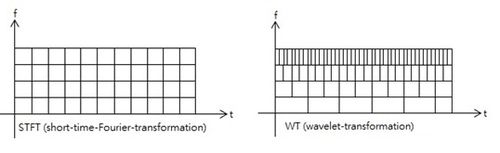
Man kann sich nun anhand der simplen Haar-Wavelet klar machen, dass für die einzelnen "Stufen" der Wavelet-Transformation gilt:
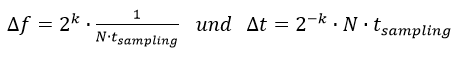
Wobei man wiederrum sieht, dass die Unschärfe innerhalb der einzelnen Stufen erhalten bleibt.
Ich habe mich daran versucht, die FWT (fast wavelet transformation) umzusetzen, mich dann jedoch entschieden, das Rad nicht neu zu erfinden und stattdessen einen C++/CLI-Wrapper für die Wavelet2d-Library von Rafat Hussain, die wiederum die bekannte libfftw verwendet, zu schreiben. Zusätzlich habe ich eine kleine Library geschrieben, die das Ergebnis einer 1D-Wavelet-Transformation graphisch darstellt.